EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks(EfficientNet)(2019) Review

EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

 

0. 핵심 요약

Network의 깊이, 넓이, 해상도를 결정하는 공식인 Compound Scaling Method를 생성 → ConvNet의 성능 향상

기존의 ConvNet보다 약 8배 더 작고 약 6배 더 빠른 EfficientNet 제안

1. BackGround

- 기존 모델들의 Scale up 방식

1. 깊이(Depth)

가장 일반적으로 사용된 방식

다른 어려운 기법이 사용되지 않고 단순히 층을 더 많이 쌓으면 되기 때문에 많이 활용되었음

하지만, 이에 따른 부작용에는 대표적으로 Gradient Vanish 문제가 발생

이를 해결하기 위해 여러 대책이 개발되었는데, 그 중 대표적인 예시가 바로 ResNet의 Short Connection

ResNet은 깊이가 더 깊어질수록 성능이 향상되는 모습을 보였지만 여전히 부족함이 존재

그 예시로 ResNet-101과 ResNet-1000이 성능이 비슷하다는 것

위의 그림 중 가운데 그래프는 모델의 깊이에 따른 성능과 FLOPs의 변화를 보여줌

이는 깊이가 깊어질수록 성능 향상이 존재하기는 하지만 너무 깊어지게 되면 성능 향상 폭이 줄어들고 모델의 복잡도만 증가한다는 것을 입증

 

2. 넓이(Width)

모델의 용량(크기)가 작을 때 주로 사용하는 방식

넓이가 넓어질 때 모델에 주는 이점으로는 이미지에서 더욱 세밀한 특징을 포착할 수 있다는 점과 학습이 쉽다는 점이 존재

하지만 이는 반대로 말하면 고차원의 특징은 포착하기 어렵다는 점이 있고, 다른 것들에 비해 성능이 금방 수렴

위의 그림 중 왼쪽 그래프가 넓이에 따른 성능과 FLOPs의 변화를 보여줌

이 역시 깊이와 동일하게 넓이가 넓어질수록 성능 증가 폭은 줄어들고 FLOPs만 증가

 

3. 해상도(Resolution)

해상도는 이미지의 크기를 의미

우리가 직관적으로 생각해도 해상도가 증가하면 그만큼 해당 이미지에 대한 정보가 더 많이 담겨있기 때문에 성능이 향상할 것

하지만 이는 다른 것들 보다 효율이 떨어짐

해상도가 커질수록 성능은 오르지만 그만큼 FLOPs도 많이 증가한다는 단점이 존재

위 그림 중 오른쪽 그래프를 보면 이러한 경향을 띈다는 것을 확인할 수 있음

 

- 기존의 Model Efficiency 방향

Mobile Phone의 대중화로 인해, 우리가 사용하는 모델들의 경량화 작업이 필수적으로 요구되기 시작

따라서, 이를 만족하기 위해 SqueezeNet, MobileNet, ShuffleNet과 같은 모델 구조 자체를 효율적으로 만드는 모델 등장

하지만 이는 모델 구조 자체를 변경하는 방법이고 이와 다르게 모델 구조가 아닌 scale을 design 하는 방법도 등장

scale 자체를 design 하는 방법이 등장했지만, 이는 큰 모델에는 적용할 수 없고 적용하는 방식 역시 정형화 되어 있지 않음

 

- 모델 학습 시 사용된 기법들

1. RMSProp

지금까지 리뷰한 모델들은 모두 SGD 기법을 사용했지만, EfficientNet은 RMSProp을 적용

이는 Adagrad를 개선한 방법으로, Adagrad는 이전의 기울기를 모두 참고하기 때문에 예전의 기울기에 영향을 받음

하지만 RMSProp 이동 평균 기법을 적용해서 최근의 기울기만 참고하도록 개선

 

2. SiLU(Sigmoid-weighted Linear Units)

ReLU의 변형된 활성화 함수로, 기존의 ReLU에 Sigmoid를 추가한 것

 

3. AutoAugment

강화학습 기법을 활용하여, data augment 기법을 자동으로 select 해주는 모델

 

4. Stochastic Depth

확률적으로 layer를 사용할지 말지를 결정하는 방법

예시로, ResNet에서 Short Connection을 사용할 때 skip하는 layer를 사용할지 말지를 정하는 것으로 사용

2. 논문 핵심 내용

- Compound Scaling Method

해당 논문에서 가장 핵심이 되는 내용으로, 기존의 수동으로 tuning을 하면서 지정했던 깊이, 넓이, 해상도를 공식화하여 한층 더 쉽게 정할 수 있도록 한 공식

 

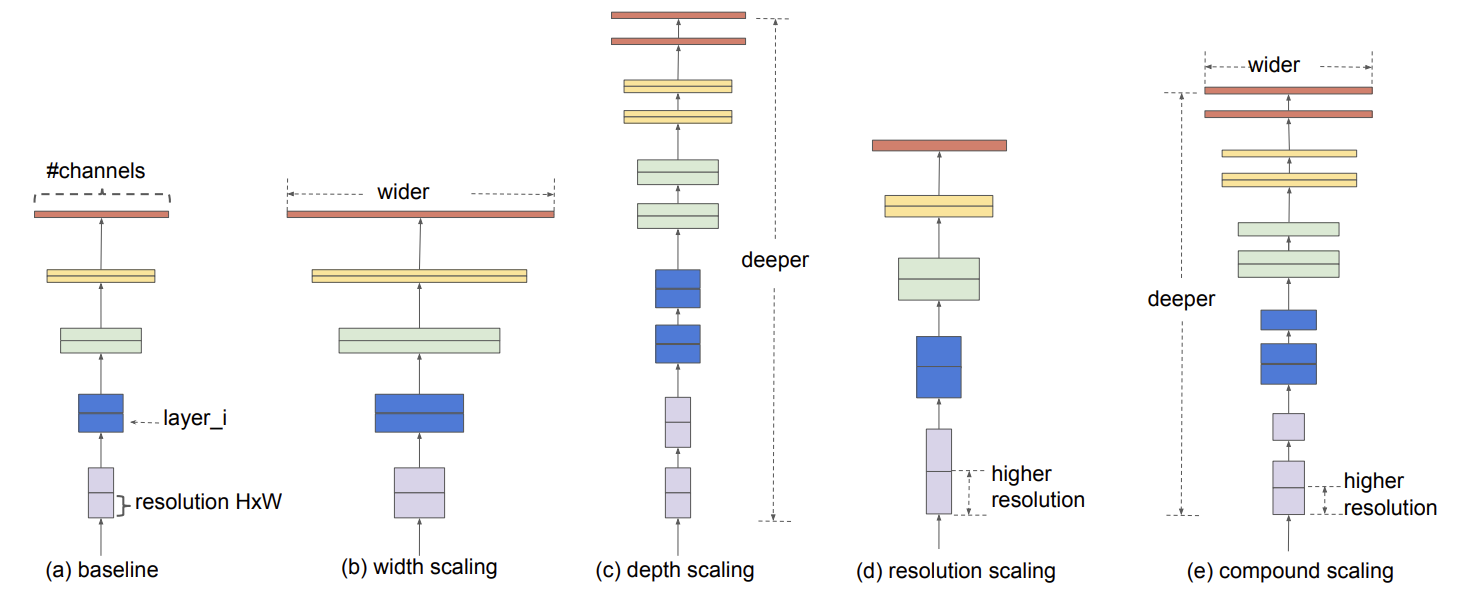
해당 이미지에서 e 사진이 논문이 제시하는 방법

다른 기법들은 모두 한가지만을 적용하여 모델을 확장하지만, e는 모든 방면에서 확장하는 것을 볼 수 있다

 

우선 논문에서는 모델의 한 layer를 다음과 같은 식으로 정립

$Y_i = F_i(X_i)$

이때 $Y_i$는 출력, $F_i$는 operator, $X_i$는 입력을 의미

$<H_i, W_i, C_i>$는 각각 이미지의 높이, 넓이, 채널 수를 의미

 

model은 여러 개의 layer를 가지고 있기 때문에 이는 다음과 같이 표현할 수 있음

$N = F_k \odot \cdots \odot F_2 \odot F_1(X_1) = \odot_{j=1, \cdots, k} F_j(X_1)$

위의 식은 입력에서 layer들의 합성곱의 연속으로 이해할 수 있음

 

기존의 ConvNet 의 연구들은 위에서 $F_i$에 해당하는 부분에서 어떻게 성능을 올릴지를 연구

하지만 본 논문에서는 이는 고정하고 깊이(L), 넓이(C), 해상도를 변경하여 성능 향상을 연구

 

따라서 해당 논문의 최종 목표는 다음과 같이 표현할 수 있음

$\underset{d, w, r}{max} ~ Accuracy(N(d, w, r))$

$N(d,w ,r) = \underset{i=1,\cdots,s}{\odot} \hat{F}_i^{d \cdot \hat{L}_i}(X_{<r\cdot \hat{H}_i, r\cdot \hat{W}_i , w\cdot \hat{C}_i >})$

Memory(N) $\leq$ target_memory

FLOPs(N) $\leq$ target_flops

 

d : 깊이와 관련된 값, w : 넓이와 관련된 값, r : 해상도와 관련된 값

이때, hat이 있는 것들은 모두 baseline network의 predefined 된 것

 

위의 식들을 해석하면, 모델의 정확도를 최대로 만드는 d, w, r를 찾는 것이 목적

d, w, r 은 모두 가중치 형태로 모델에 곱해지는 것을 볼 수 있음

또한, 메모리와 FLOPs 역시 우리의 목표보다 작은 것이 목적

 

하지만, 이 과정에서 다른 문제가 존재하는데 그것은 바로 d, w, r 이 모두 독립적이지 않다는 것 + 컴퓨팅 자원에 따라 값이 달라진다는 것

이러한 문제 때문에 기존의 다른 모델들은 위의 3가지 중 1가지 만을 골라 변경하였음

 

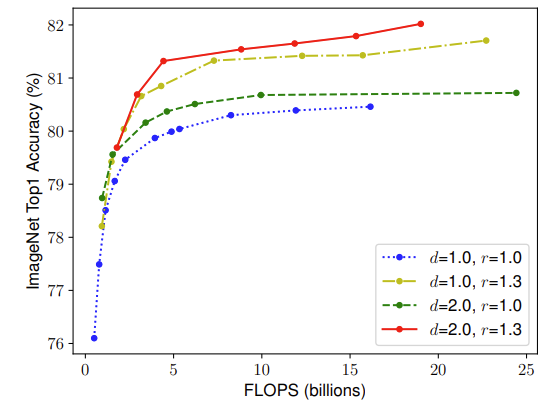
해당 그래프는 넓이를 고정한 채, 깊이와 해상도를 변화해가면서 성능과 FLOPs를 비교한 그래프

이를 보면 단순히 어떤 한 값만을 올리는 것이 아니라 두 가지의 값을 같이 적절하게 올리는 것이 중요하다는 것 발견

 

논문에서는 위와 같은 여러가지 검증 과정을 통해 총 2가지가 매우 중요하다는 것을 발견

1. 깊이, 넓이, 해상도는 모두 커질수록 성능 향상은 존재한다. 하지만 그 값이 커질수록 얻어지는 효과는 줄어든다

2. 3가지 효과에 대해 균형을 유지하는 것이 매우 중요하다

 

따라서 이를 통해 논문에서 최종적으로 제안하는 공식은 다음과 같다

$depth : d = \alpha^{\phi}, ~~ width : w = \beta^{\phi}, ~~ resolution : r = \gamma^{\phi}$

$\alpha \cdot \beta^2 \cdot \gamma^2 \approx 2$

$\alpha \geq 1, \beta \geq 1 , \gamma \geq 1$

 

이때, $\phi$는 사용자의 컴퓨팅 자원에 따라 결정하는 값

위의 식을 설명하면, 깊이와 다르게 넓이와 해상도에는 제곱이 되어 있는데 이는 해당 값은 증가함에 따라 제곱으로 FLOPs가 증가한다는 의미

따라서 최종적으로 $( \alpha \cdot \beta^2 \cdot \gamma^2)^{\phi}$ 만큼의 FLOPs가 증가

논문에서는 이를 2로 제한하였다는 것을 의미

 

- 공식 적용 순서

공식을 모델에 적용하는 순서는 다음과 같다

1. $\phi$를 1로 고정한 뒤, $\alpha, \beta, \gamma$를 small grid search를 통해 찾는다

2. 위 과정을 통해 찾은 값으로 고정하고 $\phi$값을 변화해가면서 최종 모델을 결정

 

이때 grid search를 할 때 많은 시간이 소요될 수 있으므로 최대한 작은 baseline 모델을 통해 수행

3. Model Architecture

- EfficientNet

EfficientNet은 논문에서 제시한 Compound Scaling Method의 효과를 더욱 잘 보여주기 위해 직접 만든 모델

MobileNet에서 제시한 모듈인 MBConv와 SENet에서 제시한 Squeeze-and-Excitation을 적용해서 생성

위의 두 모듈은 추후에 따로 리뷰 예정

 

최종 모델의 구성은 다음과 같다

 

- 학습 parameter

RMSProp : decay 0.9, momentum 0.9

batch norm : momentum 0.99

weight decay : 1e-5

learning rate : 0.256에서 시작, 2.4epoch 마다 0.97 만큼 감소

SiLU 활성화 함수 사용

AutoAugment 기법 적용

Stochastic depth를 0.8 비율로 적용

dropout은 모델의 크기에 따라 0.2에서 0.5 사이로 적용

4. Experiment

해당 그래프는 모델의 크기와 정확도를 동시에 표현한 그래프

EfficientNet이 다른 모델과 비교했을 때 정확도나 모델의 크기가 월등하게 좋은 모습을 볼 수 있다

 

ImageNet 데이터에 대해서 정확도를 측정한 표

비교적 유사한 정확도를 보이는 모델들과 비교했을 때 파라미터의 수가 매우 적은 것을 볼 수 있다

 

해당 표는 EfficientNet이 아닌 ResNet과 MobileNet에 Compound Scaling Method를 적용해본 표

공식을 적용했을 때 유의미한 성능 향상을 이끌어 낸 것을 볼 수 있다

 

이는 기존의 존재하는 모델과의 속도를 비교한 것인데 역시 약 6배 가량 빠른 모습을 볼 수 있다

 

이는 ImageNet 데이터에 대한 정확도와 FLOPs를 비교한 그래프

앞서 설명한 parameter 수와 유사하게 FLOPs 역시 매우 효율적인 모습을 볼 수 있다

 

이는 다양한 데이터셋에 대한 정확도와 parameter 수를 비교한 표

ImageNet 뿐만 아니라 다른 데이터에서도 동일한 경향을 보이는 것으로 보아 일반화 성능 역시 좋다는 것을 입증

 

이는 ImageNet 데이터로 학습된 모델을 pretrained 모델로 활용하여 다른 데이터에 적용해본 결과

이 역시 다른 모델들에 비해 더 좋은 정확도와 효율적인 parameter 수를 보여준다

 

이는 EfficientNet의 가장 작은 버전인 B0에 Compound Scaling Method의 효과를 보여주는 그래프

단순히 한가지만을 확장했을 때보다 공식을 적용한 방식이 더 좋은 정확도를 보여준다는 것을 입증

 

이는 CAM을 활용하여 모델이 해당 이미지를 분류할 때 어디에 집중하는 지를 보여주는 heatmap

한 가지만을 확장한 모델들보다 compound scaling을 적용한 것이 더욱 특징을 잘 파악한다는 것을 볼 수 있

5. Contribution

이 논문에서는 ConvNet 스케일링을 체계적으로 연구

네트워크의 폭, 깊이, 해상도를 세심하게 균형잡는 것인 Compound scaling method 제안

이를 통해, 모바일 크기의 EfficientNet 모델이 ImageNet 및 다섯 가지 일반적인 전이 학습 데이터셋에서 더 적은 매개변수와 FLOPs로 최첨단의 정확도를 뛰어넘을 수 있음을 보여줌

+ Comment

EfficientNet은 그동안 단순히 경험적으로 알고 있었던 것을 공식화하였음

2024년인 현재 초거대 모델의 등장으로 경량화가 매우 주목받고 있다

비록 EfficientNet은 모델의 크기를 효율적으로 키우자는 내용이지만 모든 경량화의 기반이 되는 내용이기에 필수로 알아야 하는 내용이라고 생각

추후에 MobileNet과 SENet, 더 나아가 최근 자주 사용되는 Adapter와 관련된 내용도 다뤄볼 예정이다