네이버 부스트코스 - 인공지능을 위한 선형대수 CHAPTER 3 정리 (1)

본 글은 해당 강의를 참고하여 작성하였습니다.

인공지능을 위한 선형대수

 

Least Squares Problem 소개

1. Motivation for Least Squares

다음과 같이 변수는 3개이지만, 변수에 대한 방정식은 3개 이상이라고 가정해보자

이렇게 되면 식이 너무 많아져 변수 3개만으로 모든 식을 만족하는 해는 사실상 없다고 봐도 무방하다

그렇다면 우리는 해당 문제를 해결할 수 없다고 바로 결론을 내려야 할까?

 

현재 존재하는 많은 머신러닝 혹은 딥러닝 기법들은 다음과 같은 환경에 놓여있다

변수(feature)는 한정적이지만 우리가 가지고 있는 방정식(data)는 그에 비해 너무 많다

따라서, 우리는 이를 만족하는 변수를 정확한 정답은 없더라도 정답에 최대한 근사하는 값을 찾고자 한다

 

이러한 근사한 값을 찾고자 하는 것이 Least Squares의 목표라고 할 수 있다

2. Inner Product

Inner Product(내적)이란, 다음과 같은 계산을 말한다

$u, v \in \mathbb{R}^n$이 있을 때, $u \cdot v = u^Tv$ 와 같은 것을 내적이라고 한다

이는 두 벡터를 원소 곱 하여 모두를 더하는 계산을 의미하는 데 행렬 표현으로는 위와 같이 표현할 수 있다

 

내적의 성질은 다음과 같다

a) $u \cdot v = v \cdot u$ : 교환 법칙

b) $(u+v) \cdot w = u \cdot w + v \cdot w$ : 분배 법칙

c) $(cu) \cdot v = c(u \cdot v) = u \cdot (cv)$ : 상수 배

d) $u \cdot u \geq 0,~and ~ u \cdot u = 0$ if and only if $u=0$

 

위의 여러 성질 중 b, c를 통해 다음과 같은 성질을 유도해낼 수 있다

$(c_1u_1 + \cdots + c_pu_p) \cdot w = c_1(u_1 \cdot w) + \cdots + c_p(u_p \cdot w)$

이는 내적 후 선형 결합을 하거나, 선형 결합 후 내적을 수행하거나 모두 계산 결과는 동일하다는 것을 의미한다

3. Vector Norm

Norm이란, 벡터의 길이를 나타내는 단어로써 수식으로는 다음과 같이 표현된다

$||v|| = \sqrt{v \cdot v} = \sqrt{v_1^2 + v_2^2 + \cdots + c_n^2} ~and~ ||v||^2 = v \cdot v$

해당 그림을 보면 알 수 있듯이, 각 원소의 제곱을 더해 제곱근을 취하는 것으로 벡터의 길이를 구할 수 있다

이에 더해 특정 벡터 길이에 상수배를 하는 것은 다음과 같이 표현할 수 있다

$||cv|| = |c|~||v||$ 

4. Unit Vector

단위 벡터(Unit vector)란, 길이가 1인 벡터를 의미

주로 특정 벡터를 정규화하면 단위 벡터가 되며, 이가 가지는 의미는 벡터의 방향은 유지한 채 길이만 변경한다는 의미

아래와 같은 방식으로 정규화 수행

$u = {1 \over ||v||} v$

5. Distance between Vectors in $\mathbb{R}^n$

두 벡터 사이의 거리를 구하는 공식은 다음과 같다

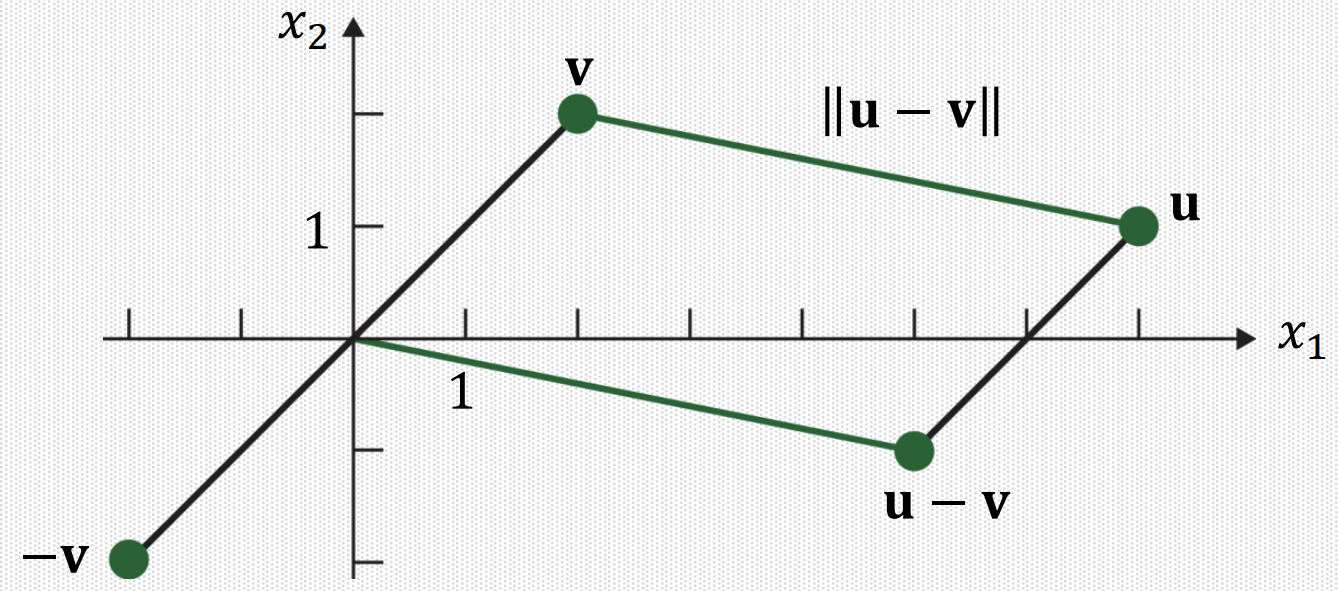
$dist~(u, v) = ||u-v||$

이를 그래프로써 표현하면 다음과 같다

6. Inner Product and Angle Between Vectors

내적 연산은 다음과 같이 norm과 각도의 곱으로도 표현할 수 있다

$u \cdot v = ||u||~||v||cos\theta$

7. Orthogonal Vectors

orthogonal(수직)인 벡터들은 특이한 성질을 가지고 있는데, 바로 내적 연산을 수행했을 시 0이 된다는 것이다

위의 내적 연산을 보면 $cos\theta$가 존재하는데, cos 은 90도에서 0 값을 가지기 때문에 내적이 0이 되는 것

8. Least Squares

동일한 문제에 대해서 다음과 같이 서로 다른 x 2개가 존재한다고 생각해보자

과연 두 x 중 어떤 것이 더 정확한 정답이라고 할 수 있을까?

 

특정 관점에서는 아래의 x가 더 많은 정답을 맞췄기 때문에 더 정확하다고 생각할 수 있다

이는 classification에서는 유용하지만 regression에서는 유용하지 않은 방법이다

 

우리가 보고자 하는 Least Squares에서는 다음과 같이 두 x를 비교한다

즉, 정답 값과 예측 값의 차이의 제곱을 모두 더해 최종 오차를 계산하는 방법이다

해당 방법을 활용하면 아래보다 위의 x가 더 정확한 정답이라고 판단하게 된다

 

이처럼 정답과 예측값의 차이의 제곱 합을 통해 오차를 결정하는 것을 Least Squares Problem이라고 하며, 수식으로 표현하면 다음과 같다

$\hat{x} = arg~\underset{x}{min} ||b-Ax||$

해당 식은 선형 시스템에서 Least Squares를 표현한 것이며, 위의 과정과 동일한 것을 수행한다

 

Least Squares Normal Equation

1. Geometric Interpretation of Least Squares

위에서 살펴본 Least Squares를 기하학적인 의미로 다시 살펴보자

다음과 같은 공간이 있다고 생각해보자

우리가 풀어야 하는 문제는 $Ax$로 $b$를 정확하게 맞추는 것이다

하지만 위의 그림처럼 b가 A의 span 안에 존재하지 않는다면 정확한 정답은 맞출 수 없다

그렇다면 A의 span 안에서 b에 가장 가까운 위치는 어딜까?

바로 b에서 A의 열공간을 향해 수직으로 내린 직선과 공간이 만나는 지점이 바로 최소 거리인 점이 될 것이다

따라서, 우리는 b를 맞출 수는 없으니 가장 유사한 위치인 $\hat{b}$를 맞추고자 하는 것이다

 

그러면 $\hat{b}$는 어떻게 구할 수 있을까?

바로 "수직"인 점을 활용하면 해당 점을 쉽게 구할 수 있다

$\hat{b}=A\hat{x}$ 라고 할 때, $b-A\hat{x}$는 열공간 A와 수직을 이룰 것이다

그렇다는 것은 A와 $b-A\hat{x}$를 내적한 결과가 0이 된다는 것을 의미하고 이를 행렬 표현으로 바꾸면 다음과 같다

$A^T(b-A\hat{x})=0$

$A^TA\hat{x}=A^Tb$

이 식을 새로운 선형 시스템이라고 생각하면, $Cx = d$와 같이 표현할 수 있다

만약, $C=A^TA$가 역행렬이 존재한다면, 우리는 위의 식을 다음과 같이 표현할 수 있을 것이다

$\hat{x}=(A^TA)^{-1}A^Tb$

 

이제 기하학적인 의미로 파악했으니, 실제 행렬 표현으로는 어떻게 위와 동일한 식을 유도하는지 확인해보자

$\hat{x} = arg~\underset{x}{min}||b-Ax||^2$

$=arg~\underset{x}{min}(b-Ax)^T(b-Ax) = b^Tb - x^TA^Tb - b^TAx + x^TA^TAx$

우리는 x의 최소값을 알고 싶은 것이기 때문에 위의 식에 x에 대해 미분을 진행한다

$-A^Tb - A^Tb + 2A^TAx=0 \Leftrightarrow A^Tb$

따라서, 이 역시 마찬가지로 $A^TA$가 역행렬이 존재한다면 다음과 같이 표현할 수 있다

$\hat{x}=(A^TA)^{-1}A^Tb$